Mathematics
Mathematics is a group of related sciences, including algebra, geometry, and calculus, concerned with the study of number, quantity, shape and space and their interrelationships by using a specialized notations.
(Mathematical notations include relatively simple symbolic representations, such as the numbers 0, 1 and 2; variables such as x, y and z; function symbols such as sin; operator symbols such as “+, -, x etc relational symbols such as “<“,)
Nursing Mathematics/Importance of Mathematics in Nursing
Nursing mathematics reviews and practices basic mathematical skills that are tailored to the needs of a professional nurse.
Nurses, in their daily practices, deal with many problems in which there is use of mathematical knowledge.
It is truth that math is incorporated into the daily lives of the health care professionals. Doctors and nurses use math when they write prescriptions or administer medications.
Mathematics plays a vital role in medicine. Since people’s lives are involved, it is crucial that nurses and doctors be really accurate with their mathematical calculations.
For example,
- If we have to give 2/3 tablet to a child, as in each country as a nurse we deal with different people and all of them do not understand the meaning of 2/3. A nurse should know that what does 2/3 means?

- If we have to infuse an IV infusion in some particular time, what should be the speed of drip i.e. how many drops/minutes? For example, according to the client’s need and his condition, a different flow rate is used.
- Conversion of one system into the others. If a nurse does not know conversion factors between different quantities, then how can he/she be able to convert these? For example, if a nurse does not know that how many kilograms in a pound and also the use of multiplication and division (mathematical operations), then it is not possible to convert pound into kilogram or kilogram into pound.

- Medication dosage calculations etc are some such problems, which can be solved by nursing mathematics. Especially in pediatric nursing and intensive care unit nursing, it becomes more important than other areas.
- It’s easy to figure out how to calculate the correct dose in your hand if the physician order calls for 25 milligrams, but the tablet comes in a 50 milligram. You simply give half the tablet. However, if the medication to be given is based on the patient’s weight in milligrams per kilogram, then you’d need to multiply in order to find out the correct dose.


- The reason understanding math is so important is because the wrong dose could mean death of the patient. According to All Experts, that is why it’s so important nurses know how to calculate the correct dose. Normally, it’s the pharmacist who does the calculations. However, if the pharmacy is unavailable to do the calculating, then the nurse would have to know how to do it.
Describe Fraction
1.1 Fraction
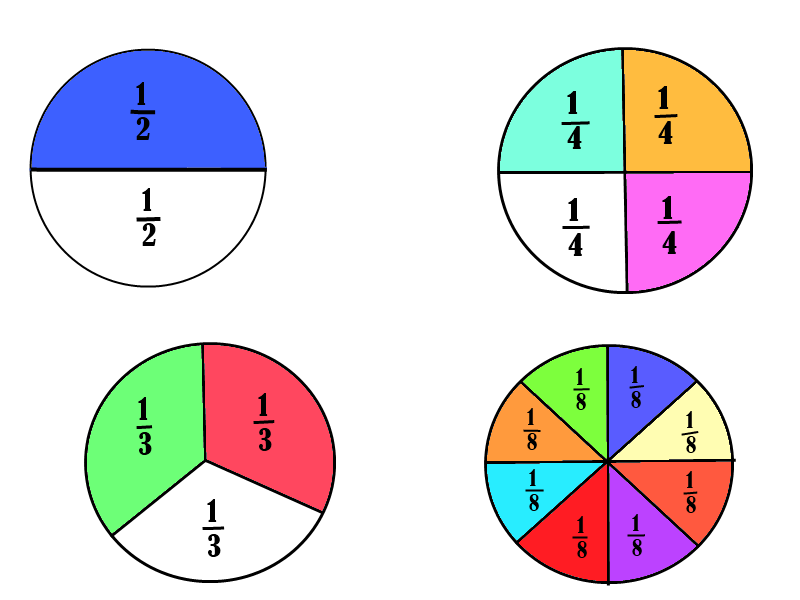
A number that expresses the relationship of one or more equal parts to the total number of equal parts in one unit (or one group) is called a fraction.
The common fraction consists of two numerals, one above the other, separated by a fraction bar.
For example, 2/3, 4/6, ½, ¾ etc are fractions.
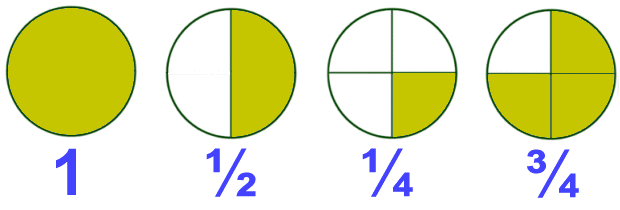
The meaning of common fraction
A common fraction is:
PART OF A WHOLE NUMBER
The fraction 2/3 (two-thirds) means that 2 out of 3 equal parts of one whole are being considered.
ONE NUMBER DIVIDED BY THE ANOTHER
The fraction 2/3 (two-thirds), read from top to bottom, means 2 divided by 3, 2 ÷ 3, or 3∫2.
A PRODUCT OF MULTIPLICATION
The fraction 2/3 (two-thirds) means that there are 2 of the thirds, or (2 X 1/3).
Example – 1 (while —- unit)
¾ of the square is shaded
¼ of the square is unshaded
4/4 is one whole square.
Example –2 (while —- group)
3/5 of the group is shaded
2/5 of the group is unshaded
5/5 is one whole group.
Exercise:
Express each of the following in three different ways
- ¾
- ½
- 3/8
B. Write fractions to express the shaded and unshaded portions of each unit or group
1.
2.
Denominator, Numerator, and Fraction Bar
A common fraction has a denominator, numerator, and a fraction bar. The denominator and numerator are called the terms of the fraction. The fraction bar represents the operation of the division.
¾
Denominator
Numerator
Fraction Bar
Denominator
The DENOMINATOR tells:
- The TOTAL number of EQUAL parts in ONE whole the SIZE of each equal part in one whole
- In fraction/ 2/3, the denominator of 3 means 3 equal parts in one whole the size of each part is one-third (1/3).
- If the denominator is 1, it means that one whole has one equal part, and that part has the size of one whole. Then 2/1 is read as “two wholes”.
Note:
The denominator of a fraction cannot be zero. It is impossible for zero parts to make one whole and it is impossible to divide by zero.
Numerator
A number (up above the fraction bar) gives an important piece of information.
The NUMERATOR tells the NUMBER of EQUAL parts being used, talked about, or considered.
- In fraction 2/3, numerator 2 means 2 equal parts are being talked about (out of total of 3 equal parts in one whole).
Fraction bar
In mathematics, the symbol ÷ means “divided by”. Read a fraction from top to bottom when reading as an expression of division.
7/8 = 7 divided by 8 = 7÷ 8 = 8∫7
Exercise:
Fill in the blanks about each fraction.
Look at the fraction.
- ¾
- What is the total number of equal parts in whole? __________
- What is the size of each part? __________
- How many parts are being talked about? __________
- The numerator is __________
- The denominator is __________
TYPES/KINDS OF FRACTION
1. PROPER FRACTIONS
A fraction is called proper fraction if the numerator is smaller than the denominator. The value of proper fraction is less than one.
For example: ¾, ¼, 4/5.
2. IMPROPER FRACTION
A fraction is called improper fraction if the numerator is larger than or equal to the denominator. The value of the fraction is equal to one or more than one.
For example: 4/4, 5/1, 7/4.
Note: Every natural number can be written as a fraction in which 1 isitss denominator. For example, 2 = 2/1, 25 = 25/1, 53 = 53/1, etc. So, every natural number is an improper fraction.
Mixed fraction:
A combination of a proper fraction and a whole number is called a mixed fraction.
2 1/3, 4 5/2, 11 1/10 and 7 5/11 are examples of mixed fractions.
In other words:
A fraction which contains two parts: (i) a natural number and (ii) a proper fraction, is called a mixed fraction, e.g., 3 2, 7 3 etc.
5 4
In 3 2/5, 3 is the natural number part and 2/5 is the proper fraction part.
In Fact, 3 2/5 means 3 + 2/5.
EQUIVALENT FRACTION:
Fractions, which have the same value but look different, are called equivalent (equal) fractions. The written form of the fraction changes, but the value of the fraction remains the same.
For example:
½, 2/4, 4/8, 8/16 are equivalent fractions.
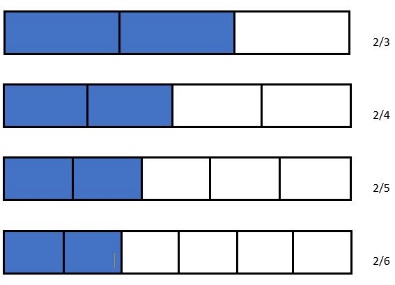
COMPARING FRACTIONS
When comparing fractions, these symbols are used
= is equal to 7/8 = 14/16
> is greater than 1/3 > 3/14
< is less than 3/10 < 7/8.
Note:
- If the denominators are the same, the fraction with larger numerator has the greater value.
For example, in the following fractions 5 is greater numerator so the fraction 5/8 has greater value than 3/8. Its mean 5/8 > 3/8.
Another method for comparison fractions:
For example, we have to compare 5/8 and 3/8
Step I Write 0 after numerators in both fractions. These will be 50/8 and 30/8
Step II simplify these two up to one time only, answers will be 6 and 3 respectively so first is larger value that’s why 5/8 > 3/8
- If the numerators are the same, the fraction with the smaller denominator has the greater value.
For example: 2/4 > 2/ 8, ½ > ¼.
Another method for comparison fractions:
For above fractions 2/4 and 2/8
Step I Write 0 after numerators in both fractions. These will be 20/4 and 20 /8
Step II simplify these two upto one time only, answers will be 5 and 2 respectively so first is larger value that’s why 2/4 > 2/8
- To compare 2/3 and ¾, a common denominator for both fractions must be found. Rewrite each fraction as an equivalent fraction using the common denominator.
2 X 4 = 8 3 X 3 = 9
——- — ——– —–
3 X 4 = 12 4 X 3 = 12
Now comparing 2/3 and ¾ is the same as 8/12 and 9/12.
Therefore 2/3 < ¾ because 8/12 < 9/12.
Another method for comparison fractions:
For example we have to compare 2/3 and 3/4
Step I Write 0 after numerators in both fractions. These will be 20/3 and 30/4
Step II simplify these two upto one time only, answers will be 6 and 7 respectively so second is larger value that’s why 3/4 > 2/3 OR 2/3 < 3/4
1.2 Decimal or Decimal Fraction
Decimal is a fraction that has an unwritten denominator of a power of 10. It is indicated by a decimal point to the left of the numerator; .2 = 2/10 (Collins Concise Dictionary)
Decimal fractions represent common fractions that have denominators of 10, 100, 1000, or some power of 10. To the left of decimal points are whole numbers and to the right of the decimal points are fractional parts.
In
1.75, 1 is the whole number which is to the left of the decimal point while 75 is the fractional part as it is to the right of decimal point.
In decimal fractions, a zero is written to the left of the decimal point to indicate clearly that there are no whole numbers in the decimal, just fractional parts, for example, 0.75 (not .75).
First look at the fractional parts. Let’s add a zero to the right of the decimal point.
| Decimal | Common fraction | Words |
| 0.6 | 6/10 | 6 tenths |
| 0.60 | 60/100 | 60 hundredths |
| 0.600 | 600/1000 | 600 thousandths |
Notice here that adding zeroes after the last digit to the right of the decimal point does not change the value.
Let’s put the zero in different position:
| Decimal | Common fraction | Words |
| 0.7 | 7/10 | 7 tenths |
| 0.07 | 7/100 | 7 hundredths |
| 0.007 | 7/1000 | 7 thousandths |
Adding zeroes between the decimal point and the first number to the right of the decimal point does change the value.
Division of Decimals
Dividend = Quotient
Divisor
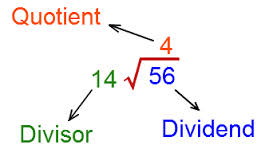
Remember: Quotient is another name for Answer. They’re one and the same.
1.2.1 Division of Whole by Decimal
If the divisor is not a whole number, move the decimal point the same number of places to the right in the divisor and the dividend so that the divisor becomes a whole number. Place the decimal point in the quotient directly above the new decimal point in the dividend. Then divide.
A. 7 ÷ 1.75 = 7 / 1.75
1.75∫7.00 (4
700
0
Second Method:
- Make the divisor (1.75) a whole number by multiplying 100 times.
- Multiplying the dividend (7) by the same number, 100
- Place the decimal point in the quotient (your answer).
- Divide.
7 x 100 = 700 = 4.
1.75 100 175
Solve the following:
A. 19 ÷ 1.2 (15.83)
B. 15 ÷ 0.7 (21.42)
On the Job practice
Q1. How many 0.5-gram doses can be obtained from a 4-gram vial of medication? (8 doses)
Q2. How many 0.25-gram doses can be obtained from a 2-gram vial of medication? (8 doses)
1.2.2 Division of decimal by whole
If the divisor is a whole number, place the decimal point in the quotient directly above the decimal point in the dividend. Then divide. Look at the following example:
- 1.26 ÷ 6 = 1.26 / 6 6∫1.26(0.21
12__
6
6
Solve the following:
A. 0.19 ÷ 12 (0.015)
B. 8.89 ÷ 7 (1.27)
On the Job practice
Q. A total of 270.9 grams of meat is to be served in three meals. How many grams of meat should be served in each meal? (90.3 gram)
Q. A total of 1.50-grams of medication is given in 3 doses. How many grams should be given per dose? (0.50 gram per dose)
1.2.3 Division of Decimal by Decimal
A. 14.48 ÷ 0.4 = 14.48 / 0.4
- 0.4∫14.48(36.2
12__
2 4
2 4
08
08
0
Second Method:
- Make the divisor (0.4) a whole number by multiplying by 10.
- Multiply the dividend (14.48) by the same number, 10.
- Place the decimal point in the quotient.
- Divide.
Solve the following:
- 12.24 ÷ 0.6 (20.4)
- 15.5 ÷ 1.5 (10.33)
On the Job practice
- A container holds 16.25 milliliters of medication. How many 1.25 milliliter doses can be administered from the container? (13 doses)
- The total prescribed dosage of medication is 4.5 grams. How many 1.5-gram tablets need to be administered? (3 tablets)
1.3 Percentage
Percent or percentage is another kind of fraction that always has a denominator of 100.
1.3.1 The Meaning of Percentage: –
Percent means “per 100” or “÷ 100”.
Remember that the fraction bar means “divided by”.
6% = 6 percent = 6 per 100 = 6 / 100 6 divided by 100
25% = 25 percent = 25 per 100 = 25 / 100
100% = 100 percent = 100 per 100 = 100 / 100
Dividing by 100 results in “hundredths” as can be seen. Another way of saying percent is hundredths.
1% = 1 percent = 1/ 100 = 1 hundredths
50% = 50 percent = 50/ 100 = 50 hundredths
75% = 75percent = 75/ 100 = 75 hundredths
Common fractions can be equal to one (7/7), less than one (1/7), more than one (15/7). Similarly, decimals can be equal to one (1), less than one (0.5), more than one (1.5).
And percentage too, can be equal to one (100% = 100/100), less than one (30% = 30/100), more than one (150% = 150/100).
1.3.2 Conversion of percent to fractions:
25% = 25/100 = ¼
50% = 50/100 = ½
75% = 75/100 = 3/4
125% = 125/100 = 1 25/100 = 1 ¼
1.3.3 Conversion of percent to decimals:
4% = 4/100 = 0.04
35% = 35/100 = 0.35
100% = 100/100 = 1.
125% = 125/100 = 1.25
1.3.4 Conversion of Fraction to Percentage
A common fraction is converted to percentage in TWO STEPS
Step -1. Express the fraction as decimal (divide the numerator by the denominator)
Step -2. Change the decimal to a percent by multiplying by 100 and add a percent sign (%)
¼ = 1÷ 4 = 0.25 x 100 = 25 %
3/8 = 3 ÷ 8 = 0.375 x 100 = 37.5 %
2/5 = 2 ÷ 5 = 0.4 x 100 = 40 %
Change the common fraction to its equivalent percentage
a. ½ (50%)
b. 5/8 (62.5%)
c. ¾ (75%)
1.3.5 Conversion of Decimal to Percentage:
To convert a decimal to a percent, multiply by 100. Move the decimal point two places to the right and add a percent sign.
0.125 = 0.125 x 100 = 12.5 %
3.9 = 3.9 x100 = 390 %
0.75 = 0.75 x 100 = 75 %
Express the following as an equivalent percent:
-
- 0.50 (50%)
- 0.005 (0.5%)
1.4 Formula of Percentage:
Percent (%) = Numerator X 100
Denominator
1.4.1 How to calculate percentage
Suppose we have to know the percentage of ½
Suppose the percent of ½ is A % then
A = ½ X 100 = 0.5 X100 = 50%
1. Suppose you got 740 marks out of 850 in your SSC. What is your percentage in SSC?
Using above formula
A = 740/850 X 100 = 0.87 X 100 = 87%.
2. What is the percentage of the solution if you have 50 gram of solute in 1000 mL of solution? (Answer 5%)
Solve it yourself using the same method.
Solution Strength as Percent:
Percent strength describes the amount that was dissolved in a liquid to form the solution.
- A 5% solution made with pure drug (liquid form) means 5 ml (solute) of pure drug in 100 ml (Solvent) of solution.
5% Solution = 5ml/100 ml
- A 5% solution made with pure drug (dry form) means 5 gm(solute) of pure drug in 100 ml (Solvent)of solution.
5% Solution = 5 gm/100 ml
In clinical life we use iv fluids like Inj:5% D/W 1000 cc, or Inj:10% D/W 1000 cc
Its mean in Inj: 5% D/W, there are 5 grams of dextrose i.e. glucose in 100 mL of Distilled water so there will be 50 gram of glucose in 1000 cc of distilled water or there is 50gram of glucose in 1000 cc in this drip, similarly in 10% D/W, there is 100gram of glucose in 1000 cc in this drip.
Conversion of Decimal to Fraction
Decimal fractions can be converted into common fractions by dropping the decimal point to find numerator and using the correct denominator.
Example:
A. 0.15 Drop the decimal point to find numerator 15. The proper denominator (100) will have as many zeroes as there are decimal places to the right of the decimal point. 0.15 = 15/100
B. 0.2 Drop the decimal point to find numerator 2. The proper denominator (10) will have as many zeroes as there are decimal places to the right of the decimal point. 0.2 = 2/10
C. 0.005 Drop the decimal point to find the numerator 5. The proper denominator (1000) will have as many as zeroes as there are decimal places to the right of the decimal point. 0.005 = 5/1000
2. Apply four fundamental operations on fraction, decimal and percentage:
Addition, Subtraction, Multiplication and Division of Fractions
Addition of Fractions:
- Add 3/8 + 2/8 + 5/8
Solution: first of all we take Least Common multiple (LCM), as denominator is same then this is the LCM
3/8 + 2/8 + 5/8
3 + 2 + 5 = 10/8 = 5/4 = 1 ¼ Answer
8
as this is not a proper fraction and Answer should have proper fraction so we convert it into mixed fraction.
- Add 2/3 + ¾ + 1/6
Solution: first of all, we take Least Common multiple (LCM), as denominators are different then we use the following method.
2 3,4,6
2 3,2,3 3 3,1,3
1,1,1
Hence 2x2x3=12 is LCM, each of 3,4, and 6 can multiply 12 completely without remainder.
2/3 + ¾ + 1/6
8 + 9 + 2 = 19/12 = 1 7_ Answer.
12 12
- Add 3 3 + 4 5
4 6
Note: Mixed numbers are first written as improper fraction (6 ½ = 13/2). Whole numbers are written as fraction by putting whole number over the denominator 1. Whether there is any of four operations.
- Solution: 3 3 + 4 5
4 6
Make improper fraction
- 3 ¾ Multiply 4 and 3, it wl be 12 now add 3(numerator) it will be 15. Now rewrite it as 15/4
- similarly change 4 5/6 and write as 29/6
Now add 15/4 and 29/6, same as Q. No.2.
Subtraction of Fractions:
- Subtract 1/8 from 7/8
Solution: first of all we take Least Common multiple (LCM), as denominator is same then this is the LCM.
7/8 – 1/8
7 – 1 = 6/8 = ¾ Answer (answer should in minimum fraction)
8
Similarly do the following yourself
- Subtract 9/16 from ¾
- Subtract 7 7 _ 3
8 4
Multiplication of Fractions
-
- Multiply 15/8 and 7/30
15 X 7 = 7 Answer
8 30 2 16
-
- Multiply ½ and ¼
- Multiply 3, 2/9, and 9/10.
Division of Fractions:
Division involves the use of a reciprocal (or inverse). The reciprocal of a fraction is its “flip.” Change mixed numbers and whole numbers to their equivalent improper fractions first. Then find the reciprocal of the divisor by inverting (flipping) it.
- Divide 2 ½ by ¼ or 2 ½ ÷ ¼
Or 5/2 ÷ ¼
2
5 X 4 = 5 X 2 = 10 Answer
2 1
- Divide ¾ by ¼
- Divide 8 by 4 1
5
Addition, Subtraction, Multiplication and Division of Decimal
Addition of Decimal Numbers:
To add any decimal numbers, line up the decimal points. To avoid confusion, add zeroes after the last digit to make all of the decimal fractions’ same length. This does not change the value of the decimal fraction.
Find the sum of the following
(keep in mind that you have to keep the numbers according to digit place i.e. unit, 10th, 100th etc as kept in Q.No. below)
- 8.45 + 7.98
8.45
7.98
16.43 answer
- 6.94 + 0.5 + 17.102 + 8
Subtraction of Decimal Numbers:
- 8.4 – 0.7
- 7.8 – 3.92
- 6 – 3.45
On the Job
- A patient receives the following doses of medication: 1.75 milliliters, 2.5 milliliters, and 2 milliliters. What is the total dosage? (6.25 mL)
- A vial contains 3.5 milliliters of medication. An injection of 2.25 milliliters is withdrawn from the vial into a syringe. How much medication remains in the vial? (1.25 mL)
- Patient Ali weighed 65.95 kilograms (kg) 2 months ago. His weight then increased by 0.9 kg one month, and 1.58 kg the next month. What is his current weight? (68.43 Kg)
- A patient is to receive a dosage of 2.5 milligrams (mg) and has been given 1.75 mg. What additional amount of medication must be administered? (0.75mg)
Multiplication of Decimals
Observe the names given to the parts of a multiplication problem.
Factor X Factor = Product
0.2 X 0.4 = 0.08
A. 6.51 (2 decimal places)
X .2 (1 decimal place)
1.302 (3 decimal place)
- Multiply 30.7 and 1.6 (49.12)
- Multiply 7.9 and 12 (94.8)
On the JOB
- A patient is given 0.09 kilogram of meat for each meal. How many kilograms of meat are served in nine meals? (0.81 kg)
- A container holds 10.75 liters of ethyl alcohol. How much alcohol is in six of these containers? (64.5 liters)
Divisions of Decimals:
Already done previously
- Apply the percentage formula in different word problems:
- 1 out of 45 patient received insulin. —— %
Solution:
Using the formula for percent = numerator/denominator X 100
1/ 45 X 100 = 2.22 % patients received insulin.
- 75 out of 125 patients required follow up visits ——– % (60 %)
- 1 out of 110 patients received a blood transfusion. —– % (0.90 %)
- Nearly 0.07 of the patients stayed fewer than two days. —— %
Solution:
0.07 = 7/100 X 100 = 7%
5. Only 0.005 of the patients remained in the hospital for more than two weeks.
—- % (0.5 %)
