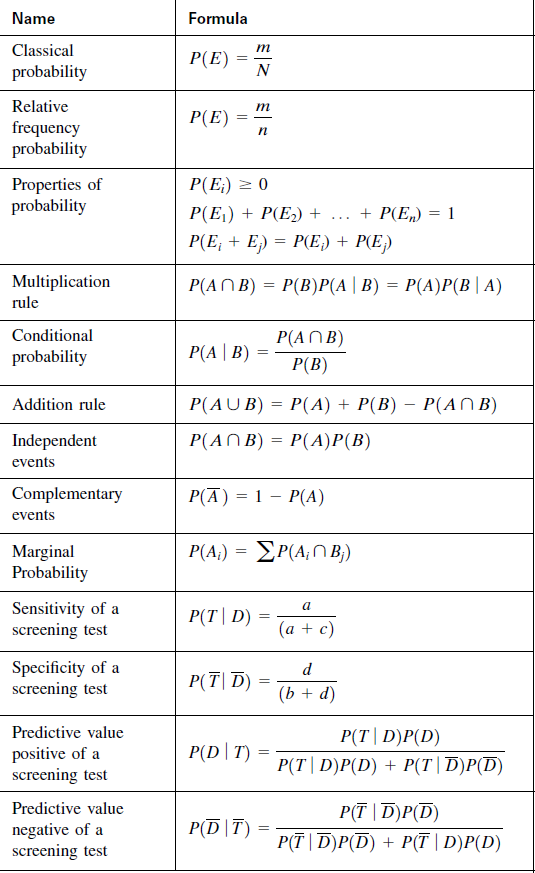
INFERENTIAL STATISTICS

Posted on June 1, 2020 by Bherulal

INFERENTIAL STATISTICS

Statistical inference is the procedure by which we reach a conclusion about a population on the basis of the information contained in a sample drawn from that population. It consists of two techniques:

Estimation of parameters
Hypothesis testing

ESTIMATION OF PARAMETERS

The process of estimation entails calculating, from the data of a sample, some statistic that is offered as an approximation of the corresponding parameter of the population from which the sample was drawn.

Parameter estimation is used to estimate a single parameter, like a mean.

There are two types of estimates

Point Estimates
Interval Estimates (Confidence Interval).

POINT ESTIMATES

A point estimate is a single numerical value used to estimate the corresponding population parameter.

For example: the sample mean ‘x’ is a point estimate of the population mean μ. the sample variance S² is a point estimate of the population variance σ². These are point estimates — a single–valued guess of the parametric value.

A good estimator must satisfy three conditions:

Unbiased: The expected value of the estimator must be equal to the mean of the parameter
Consistent: The value of the estimator approaches the value of the parameter as the sample size increases
Relatively Efficient: The estimator has the smallest variance of all estimators which could be used

CONFIDENCE INTERVAL (Interval Estimates)

An interval estimate consists of two numerical values defining a range of values that, with a specified degree of confidence, most likely includes the parameter being estimated.

Interval estimation of a parameter is more useful because it indicates a range of values within which the parameter has a specified probability of lying. With interval estimation, researchers construct a confidence interval around estimate; the upper and lower limits are called confidence limits.

Interval estimates provide a range of values for a parameter value, within which we have a stated degree of confidence that the parameter lies. A numeric range, based on a statistic and its sampling distribution that contains the population parameter of interest with a specified probability.

A confidence interval gives an estimated range of values which is likely to include an unknown population parameter, the estimated range being calculated from a given set of sample data

Calculating confidence interval when n ≥ 30 (Single Population Mean)

Example: A random sample of size 64 with mean 25 & Standard Deviation 4 is taken from a normal population. Construct 95 % confidence interval

We use following formula to solve Confidence Interval when n ≥ 30

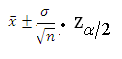
Data

= 25

= 4

n = 64

25 4/ . x 1.96

25 4/8 x 1.96

25 0.5 x 1.96

25 0.98

25 – 0.98 ≤ µ ≤ 25 + 0.98

24.02≤ µ ≤ 25.98

We are 95% confident that population mean (µ) will have value between 24.02 & 25.98

Calculating confidence interval when n < 30 (Single Population Mean)

Example: A random sample of size 9 with mean 25 & Standard Deviation 4 is taken from a normal population. Construct 95 % confidence interval

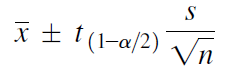
We use following formula to solve Confidence Interval when n < 30

(OR)

Data

= 25

S = 4

n = 9

α/2 = 0.025

df = n – 1 (9 -1 = 8)

t_α/2,df = 2.306

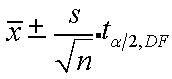
25 ± 4/√9 x 2.306

25 ± 4/3 x 2.306

25 ± 1.33 x 2.306

25 ± 3.07

25 – 3.07 ≤ µ ≤ 25 + 3.07

21.93 ≤ µ ≤ 28.07

We are 95% confident that population mean (µ) will have value between 21.93 & 28.07

Hypothesis:

A hypothesis may be defined simply as a statement about one or more populations. It is frequently concerned with the parameters of the populations about which the statement is made.

Types of Hypotheses

Researchers are concerned with two types of hypotheses

Research hypotheses

The research hypothesis is the conjecture or supposition that motivates the research. It may be the result of years of observation on the part of the researcher.

Statistical hypotheses

Statistical hypotheses are hypotheses that are stated in such a way that they may be evaluated by appropriate statistical techniques.

Types of statistical Hypothesis

There are two statistical hypotheses involved in hypothesis testing, and these should be stated explicitly.

Null Hypothesis:

The null hypothesis is the hypothesis to be tested. It is designated by the symbol H_o. The null hypothesis is sometimes referred to as a hypothesis of no difference, since it is a statement of agreement with (or no difference from) conditions presumed to be true in the population of interest.

In general, the null hypothesis is set up for the express purpose of being discredited. Consequently, the complement of the conclusion that the researcher is seeking to reach becomes the statement of the null hypothesis. In the testing process the null hypothesis either is rejected or is not rejected. If the null hypothesis is not rejected, we will say that the data on which the test is based do not provide sufficient evidence to cause rejection. If the testing procedure leads to rejection, we will say that the data at hand are not compatible with the null hypothesis, but are supportive of some other hypothesis.

Alternative Hypothesis

The alternative hypothesis is a statement of what we will believe is true if our sample data cause us to reject the null hypothesis. Usually the alternative hypothesis and the research hypothesis are the same, and in fact the two terms are used interchangeably. We shall designate the alternative hypothesis by the symbol H_AorH_1.

LEVEL OF SIGNIFICANCE

The level of significance is a probability and, in fact, is the probability of rejecting a true null hypothesis. The level of significance specifies the area under the curve of the distribution of the test statistic that is above the values on the horizontal axis constituting the rejection region. It is denoted by ‘α’.

Types of Error

In the context of testing of hypotheses, there are basically two types of errors:

TYPE I Error
TYPE II Error

Type I Error

A type I error, also known as an error of the first kind, occurs when the null hypothesis (H₀) is true, but is rejected.
A type I error may be compared with a so called false positive.
The rate of the type I error is called the size of the test and denoted by the Greek letter α (alpha).
It usually equals the significance level of a test.
If type I error is fixed at 5 %, it means that there are about 5 chances in 100 that we will reject H₀ when H₀ is true.

Type II Error

Type II error, also known as an error of the second kind, occurs when the null hypothesis is false, but erroneously fails to be rejected.
Type II error means accepting the hypothesis which should have been rejected.
A Type II error is committed when we fail to believe a truth.
A type II error occurs when one rejects the alternative hypothesis (fails to reject the null hypothesis) when the alternative hypothesis is true.
The rate of the type II error is denoted by the Greek letter β (beta) and related to the power of a test (which equals 1-β ).

In the tabular form two errors can be presented as follows:

	Null hypothesis (H₀) is true	Null hypothesis (H₀) is false
Reject null hypothesis	Type I error False positive	Correct outcome True positive
Fail to reject null hypothesis	Correct outcome True negative	Type II error False negative

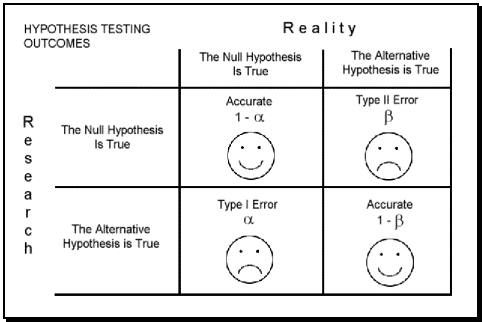
$D:\Type-I-and-II-Errors.topicArticleId-267532,articleId-267497_files\267185.png$ Graphical depiction of the relation between Type I and Type II errors

What are the differences between Type 1 errors and Type 2 errors?

Type 1 Error	Type 2 Error
A type 1 error is when a statistic calls for the rejection of a null hypothesis which is factually true. We may reject H₀ when H₀ is true is known as Type I error . A type 1 error is called a false positive. It denoted by the Greek letter α (alpha). Null hypothesis and type I error	A type 2 error is when a statistic does not give enough evidence to reject a null hypothesis even when the null hypothesis should factually be rejected. We may accept H₀ when infect H₀ is not true is known as Type II Error. A type 2 error is a false negative. It denoted by “β” (beta) Alternative hypothesis and type II error.

Reducing Type I Errors

Prescriptive testing is used to increase the level of confidence, which in turn reduces Type I errors. The chances of making a Type I error are reduced by increasing the level of confidence.

Reducing Type II Errors

Descriptive testing is used to better describe the test condition and acceptance criteria, which in turn reduces type ii errors. This increases the number of times we reject the null hypothesis – with a resulting increase in the number of type I errors (rejecting H₀ when it was really true and should not have been rejected).
Therefore, reducing one type of error comes at the expense of increasing the other type of error! The same means cannot reduce both types of errors simultaneously.

Power of Test:

Statistical power is defined as the probability of rejecting the null hypothesis while the alternative hypothesis is true.

Power = P(reject H₀ | H₁ is true)

= 1 – P(type II error)

= 1 – β

That is, the power of a hypothesis test is the probability that it will reject when it’s supposed to.

Distribution under H₀



Distribution under H₁

Power

Factors that affect statistical power include

The sample size
The specification of the parameter(s) in the null and alternative hypothesis, i.e. how far they are from each other, the precision or uncertainty the researcher allows for the study (generally the confidence or significance level)
The distribution of the parameter to be estimated. For example, if a researcher knows that the statistics in the study follow a Z or standard normal distribution, there are two parameters that he/she needs to estimate, the population mean (μ) and the population variance (σ²). Most of the time, the researcher know one of the parameters and need to estimate the other. If that is not the case, some other distribution may be used, for example, if the researcher does not know the population variance, he/she can estimate it using the sample variance and that ends up with using a T distribution.

Application:

In research, statistical power is generally calculated for two purposes.

It can be calculated before data collection based on information from previous research to decide the sample size needed for the study.
It can also be calculated after data analysis. It usually happens when the result turns out to be non-significant. In this case, statistical power is calculated to verify whether the non-significant result is due to really no relation in the sample or due to a lack of statistical power.

Relation with sample size:

Statistical power is positively correlated with the sample size, which means that given the level of the other factors, a larger sample size gives greater power. However, researchers are also faced with the decision to make a difference between statistical difference and scientific difference. Although a larger sample size enables researchers to find smaller difference statistically significant, that difference may not be large enough be scientifically meaningful. Therefore, this would be recommended that researcher have an idea of what they would expect to be a scientifically meaningful difference before doing a power analysis to determine the actual sample size needed.

HYPOTHESIS TESTING

Statistical hypothesis testing provides objective criteria for deciding whether hypotheses are supported by empirical evidence.

The purpose of hypothesis testing is to aid the clinician, researcher, or administrator in reaching a conclusion concerning a population by examining a sample from that population.

STEPS IN STATISTICAL HYPOTHESIS TESTING

Step # 01: State the Null hypothesis and Alternative hypothesis.

The alternative hypothesis represents what the researcher is trying to prove. The null hypothesis represents the negation of what the researcher is trying to prove.

Step # 02: State the significance level, α (0.01, 0.05, or 0.1), for the test

The significance level is the probability of making a Type I error. A Type I Error is a decision in favor of the alternative hypothesis when, in fact, the null hypothesis is true.

Type II Error is a decision to fail to reject the null hypothesis when, in fact, the null hypothesis is false.

Step # 03: State the test statistic that will be used to conduct the hypothesis test

The appropriate test statistic for different kinds of hypothesis tests (i.e. t-test, z-test, ANOVA, Chi-square etc.) are stated in this step

Step # 04: Computation/ calculation of test statistic

Different kinds of hypothesis tests (i.e. t-test, z-test, ANOVA, Chi-square etc.) are computed in this step.

Step # 05: Find Critical Value or Rejection (critical) Region of the test

Use the value of α (0.01, 0.05, or 0.1) from Step # 02 and the distribution of the test statistics from Step # 03.

Step # 06: Conclusion (Making statistical decision and interpretation of results)

If calculated value of test statistics falls in the rejection (critical) region, the null hypothesis is rejected, while, if calculated value of test statistics falls in the acceptance (noncritical) region, the null hypothesis is not rejected i.e. it is accepted.

Note: In case if we conclude on the basis of p-value then we compare calculated p-value to the chosen level of significance. If p-value is less than α, then the null hypothesis will be rejected and alternative will be affirmed. If p-value is greater than α, then the null hypothesis will not be rejected

If the decision is to reject, the statement of the conclusion should read as follows: “we reject at the _______ level of significance. There is sufficient evidence to conclude that (statement of alternative hypothesis.)”

If the decision is to fail to reject, the statement of the conclusion should read as follows: “we fail to reject at the _______ level of significance. There is no sufficient evidence to conclude that (statement of alternative hypothesis.)”

Rules for Stating Statistical Hypotheses

When hypotheses are stated, an indication of equality (either = ,≤ or ≥ ) must appear in the null hypothesis.

Example:

We want to answer the question: Can we conclude that a certain population mean is not 50? The null hypothesis is

H_o : µ = 50

And the alternative is

H_A : µ ≠ 50

Suppose we want to know if we can conclude that the population mean is greater than

50. Our hypotheses are

H_o: µ ≤ 50

H_A: µ >

If we want to know if we can conclude that the population mean is less than 50, the hypotheses are

H_o : µ ≥ 50

H_A: µ < 50

We may state the following rules of thumb for deciding what statement goes in the null hypothesis and what statement goes in the alternative hypothesis:

What you hope or expect to be able to conclude as a result of the test usually should be placed in the alternative hypothesis.
The null hypothesis should contain a statement of equality, either = ,≤ or ≥.
The null hypothesis is the hypothesis that is tested.
The null and alternative hypotheses are complementary. That is, the two together exhaust all possibilities regarding the value that the hypothesized parameter can assume.

T- TEST

T-test is used to test hypotheses about μ when the population standard deviation is unknown and Sample size can be small (n<30).

The distribution is symmetrical, bell-shaped, and similar to the normal but more spread out.

Calculating one sample t-test

Example: A random sample of size 16 with mean 25 and Standard Deviation 5 is taken from a normal population Test at 5% LOS that; : µ= 22

: µ≠22

SOLUTION

Step # 01: State the Null hypothesis and Alternative hypothesis.

: µ= 22

: µ≠22

Step # 02: State the significance level

α = 0.05 or 5% Level of Significance

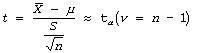Step # 03: State the test statistic (n<30)

t-test statistic

Step # 04: Computation/ calculation of test statistic

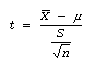
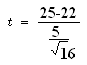
Data

= 25

µ = 22

S = 5

n = 16

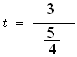
t _calculated = 2.4

Step # 05: Find Critical Value or Rejection (critical) Region

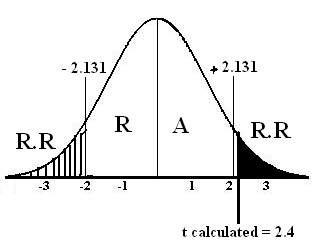
For critical value we find and on the basis of its answer we see critical value from t-distribution table.

Critical value = α/2(v = 16-1)

= 0.05/2(v = 15)

= (0.025, 15)

t _tabulated= ± 2.131

t _calculated = 2.4

Step # 06: Conclusion: Since t _calculated = 2.4 falls in the region of rejection therefore we reject at the 5% level of significance. There is sufficient evidence to conclude that Population mean is not equal to 22.

Z- TEST

Z-test is applied when the distribution is normal and the population standard deviation σ is known or when the sample size n is large (n ≥ 30) and with unknown σ (by taking S as estimator of σ).
Z-test is used to test hypotheses about μ when the population standard deviation is known and population distribution is normal or sample size is large (n ≥ 30)

Calculating one sample z-test

Example: A random sample of size 49 with mean 32 is taken from a normal population whose standard deviation is 4. Test at 5% LOS that : µ= 25

: µ≠25

SOLUTION

Step # 01: : µ= 25

: µ≠25

Step # 02: α = 0.05

Step # 03:Since (n<30), we apply z-test statistic

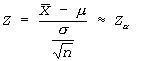
Step # 04: Calculation of test statistic

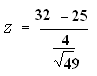
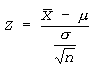
Data

= 32

µ = 25

= 4

n = 49

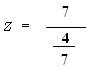
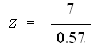
Z_calculated = 12.28

Step # 05: Find Critical Value or Rejection (critical) Region

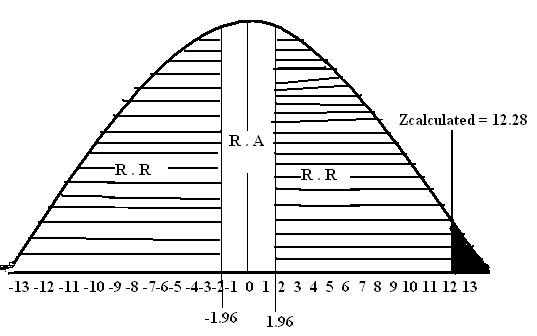
Critical Value (5%) (2-tail) = ±1.96

Z_calculated = 12.28

Step # 06: Conclusion: Since Z_calculated = 12.28 falls in the region of rejection therefore we reject at the 5% level of significance. There is sufficient evidence to conclude that Population mean is not equal to 25.

CHI-SQUARE

A statistic which measures the discrepancy (difference) between KObserved Frequencies f_o1, f_o2… f_ok and the corresponding ExpectedFrequencies f_e1, f_e2……. f_ek

The chi-square is useful in making statistical inferences about categorical data in whichthe categories are two and above.

Characteristics

Every χ2 distribution extends indefinitely to the right from 0.
Every χ2 distribution has only one (right sided) tail.
As df increases, the χ2 curves get more bell shaped and approach the normal curve in appearance (but remember that a chi square curvestarts at 0, not at – ∞ )

Calculating Chi-Square

Example 1: census of U.S. determine four categories of doctors practiced in different areas as

Specialty	%	Probability
General Practice	18%	0.18
Medical	33.9 %	0.339
Surgical	27 %	0.27
Others	21.1 %	0.211
Total	100 %	1.000

A searcher conduct a test after 5 years to check this data for changes and select 500 doctors and asked their speciality. The result were:

Specialty	frequency
General Practice	80
Medical	162
Surgical	156
Others	102
Total	500

Hypothesis testing:

Step 01”

Null Hypothesis (H_o):

There is no difference in specialty distribution (or) the current specialty distribution of US physician is same as declared in the census.

Alternative Hypothesis (H_A):

There is difference in specialty distribution of US doctors. (or) the current specialty distribution of US physician is different as declared in the census.

Step 02: Level of Significance

α = 0.05

Step # 03:Chi-squire Test Statistic

Step # 04:

Statistical Calculation

fe (80) = 18 % x 500 = 90

fe (162) = 33.9 % x 500 = 169.5

fe (156) = 27 % x 500 = 135

fe (102) = 21.1 % x 500 = 105.5

S # (n)	Specialty	f_o	f_e	(f_o – f_e)	(f_o – f_e)²	(f_o – f_e)²/ f_e
1	General Practice	80	90	-10	100	1.11
2	Medical	162	169.5	-7.5	56.25	0.33
3	Surgical	156	135	21	441	3.26
4	Others	102	105.5	-3.5	12.25	0.116
						4.816

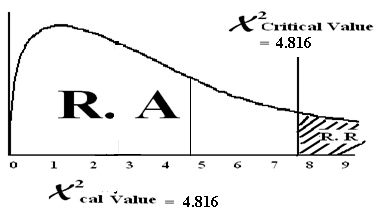χ²_cal= = 4.816

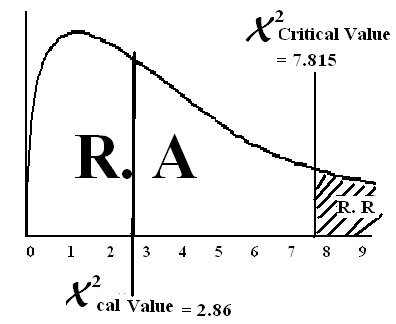
Step # 05:

Find critical region using X²– chi-squire distribution table

χ² = χ²= χ² = 7.815

^tab ^{(α,d.f) (0.05,3)}

(d.f = n – 1)

Step # 06:

Conclusion: Since χ²_calvalue lies in the region of acceptance therefore we accept the H_Oand reject H_A. There is no difference in specialty distribution among U.S. doctors.

Example2: A sample of 150 chronic Carriers of certain antigen and a sample of 500 Non-carriers revealed the following blood group distributions. Can one conclude from these data that the two population from which samples were drawn differ with respect to blood group distribution? Let α = 0.05.

Blood Group	Carriers	Non-carriers	Total
O	72	230	302
A	54	192	246
B	16	63	79
AB	8	15	23
Total	150	500	650

Hypothesis Testing

Step # 01: H_O: There is no association b/w Antigen and Blood Group

H_A: There is some association b/w Antigen and Blood Group

Step # 02:α = 0.05

Step # 03:Chi-squire Test Statistic

Step # 04:

Calculation

f_e(72) = 302*150/650 = 70

f_e(230) = 302*500/ 650 = 232

f_e(54) = 246*150/650 = 57

f_e(192) = 246*500/650 = 189

f_e(16) = 79*150/650 = 18

f_e(63) = 79*500/650 = 61

f_e(8) = 23*150/650 = 05

f_e(15) = 23*500/650 = 18

f_o	f_e	(f_o – f_e)	(f_o – f_e)²	(f_o – f_e)²/ f_e
72	70	2	4	0.0571
230	232	-2	4	0.0172
54	57	-3	9	0.1578
192	189	3	9	0.0476
16	18	-2	4	0.2222
63	61	2	4	0.0655
8	5	3	9	1.8
15	18	-3	9	0.5
				2.8674

X² = = 2.8674

X²_cal = 2.8674

Step # 05:

Find critical region using X²– chi-squire distribution table

X² = (α, d.f) = (0.05, 3) = 7.815

Step # 06:

Conclusion: Since X²_calvalue lies in the region of acceptance therefore we accept the H_Oandreject H_A. Means There is no association b/w Antigen and Blood Group

WHAT IS TEST OF SIGNIFICANCE? WHY IT IS NECESSARY? MENTION NAMES OF IMPORTANT TESTS.

1. Test of significance

A procedure used to establish the validity of a claim by determining whether or not the test statistic falls in the critical region. If it does, the results are referred to as significant. This test is sometimes called the hypothesis test.

The methods of inference used to support or reject claims based on sample data are known as tests of significance.

Why it is necessary

A significance test is performed;

To determine if an observed value of a statistic differs enough from a hypothesized value of a parameter
To draw the inference that the hypothesized value of the parameter is not the true value. The hypothesized value of the parameter is called the “null hypothesis.”

Types of test of significance

Parametric
t-test (one sample & two sample)
z-test (one sample & two Sample)
F-test.
Non-parametric
Chi-squire test
Mann-Whitney U test
Coefficient of concordance (W)
Median test
Kruskal-Wallis test
Friedman test
Rank difference methods (Spearman rho and Kendal’s tau)

P –Value:

A p-value is the probability that the computed value of a test statistic is at least as extreme as a specified value of the test statistic when the null hypothesis is true. Thus, the p value is the smallest value of for which we can reject a null hypothesis.

Simply the p value for a test may be defined also as the smallest value of α for which the null hypothesis can be rejected.

The p value is a number that tells us how unusual our sample results are, given that the null hypothesis is true. A p value indicating that the sample results are not likely to have occurred, if the null hypothesis is true, provides justification for doubting the truth of the null hypothesis.

Test Decisions with p-value

The decision about whether there is enough evidence to reject the null hypothesis can be made by comparing the p-values to the value of α, the level of significance of the test.

A general rule worth remembering is:

If the p value is less than or equal to, we reject the null hypothesis
If the p value is greater than, we do not reject the null hypothesis.

If p-value ≤ α reject the null hypothesis

If p-value ≥ α fail to reject the null hypothesis

Observational Study:

An observational study is a scientific investigation in which neither the subjects under study nor any of the variables of interest are manipulated in any way.

An observational study, in other words, may be defined simply as an investigation that is not an experiment. The simplest form of observational study is one in which there are only two variables of interest. One of the variables is called the risk factor, or independent variable, and the other variable is referred to as the outcome, or dependent variable.

Risk Factor:

The term risk factor is used to designate a variable that is thought to be related to some outcome variable. The risk factor may be a suspected cause of some specific state of the outcome variable.

Types of Observational Studies

There are two basic types of observational studies, prospective studies and retrospective studies.

Prospective Study:

A prospective study is an observational study in which two random samples of subjects are selected. One sample consists of subjects who possess the risk factor, and the other sample consists of subjects who do not possess the risk factor. The subjects are followed into the future (that is, they are followed prospectively), and a record is kept on the number of subjects in each sample who, at some point in time, are classifiable into each of the categories of the outcome variable.

The data resulting from a prospective study involving two dichotomous variables can be displayed in a 2 x 2 contingency table that usually provides information regarding the number of subjects with and without the risk factor and the number who did and did not

Retrospective Study:

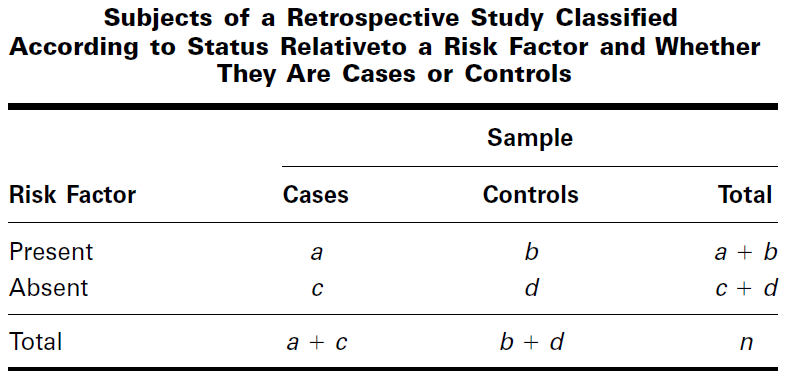
A retrospective study is the reverse of a prospective study. The samples are selected from those falling into the categories of the outcome variable. The investigator then looks back (that is, takes a retrospective look) at the subjects and determines which ones have (or had) and which ones do not have (or did not have) the risk factor.

From the data of a retrospective study we may construct a contingency table

Relative Risk:

Relative risk is the ratio of the risk of developing a disease among subjects with the risk factor to the risk of developing the disease among subjects without the risk factor.

We represent the relative risk from a prospective study symbolically as

We may construct a confidence interval for RR

100 (1 – α)%CI=

Where z_αis the two-sided z value corresponding to the chosen confidence coefficient and X²is computed by Equation

Interpretation of RR

The value of RR may range anywhere between zero and infinity.
A value of 1 indicates that there is no association between the status of the risk factor and the status of the dependent variable.
A value of RR greater than 1 indicates that the risk of acquiring the disease is greater among subjects with the risk factor than among subjects without the risk factor.
An RR value that is less than 1 indicates less risk of acquiring the disease among subjects with the risk factor than among subjects without the risk factor.

EXAMPLE

In a prospective study of pregnant women, Magann et al. (A-16) collected extensive information on exercise level of low-risk pregnant working women. A group of 217 women did no voluntary or mandatory exercise during the pregnancy, while a group of

238 women exercised extensively. One outcome variable of interest was experiencing preterm labor. The results are summarized in Table

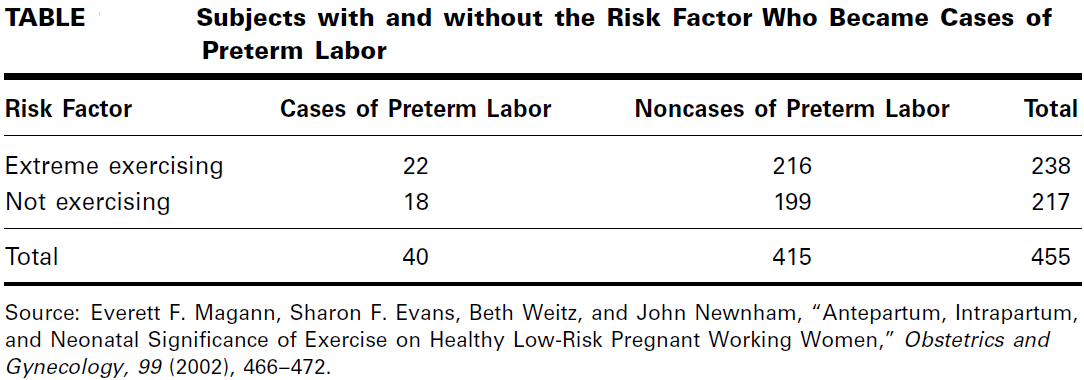
Estimate the relative risk of preterm labor when pregnant women exercise extensively.

Solution:

By Equation

These data indicate that the risk of experiencing preterm labor when a woman exercises heavily is 1.1 times as great as it is among women who do not exercise at all.

Confidence Interval for RR

We compute the 95 percent confidence interval for RR as follows.

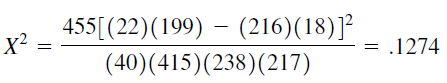
The lower and upper confidence limits are, respectively

= 0.65 and = 1.86

Conclusion:

Since the interval includes 1, we conclude, at the .05 level of significance, that the population risk may be 1. In other words, we conclude that, in the population, there may not be an increased risk of experiencing preterm labor when a pregnant woman exercises extensively.

Odds Ratio

An odds ratio (OR) is a measure of association between an exposure and an outcome. The OR represents the odds that an outcome will occur given a particular exposure, compared to the odds of the outcome occurring in the absence of that exposure.

It is the appropriate measure for comparing cases and controls in a retrospective study.

Odds:

The odds for success are the ratio of the probability of success to the probability of failure.

Two odds that we can calculate from data displayed as in contingency Table of retrospective study

The odds of being a case (having the disease) to being a control (not having the disease) among subjects with the risk factor is [a/ (a +b)] / [b/ (a + b)] = a/b
The odds of being a case (having the disease) to being a control (not having the disease) among subjects without the risk factor is [c/(c +d)] / [d/(c + d)] = c/d

The estimate of the population odds ratio is

We may construct a confidence interval for OR by the following method:

100 (1 – α) %CI=

Where is the two-sided z value corresponding to the chosen confidence coefficient and X² is computed by Equation

Interpretation of the Odds Ratio:

In the case of a rare disease, the population odds ratio provides a good approximation to the population relative risk. Consequently, the sample odds ratio, being an estimate of the population odds ratio, provides an indirect estimate of the population relative risk in the case of a rare disease.

The odds ratio can assume values between zero and ∞.
A value of 1 indicates no association between the risk factor and disease status.
A value less than 1 indicates reduced odds of the disease among subjects with the risk factor.
A value greater than 1 indicates increased odds of having the disease among subjects in whom the risk factor is present.

EXAMPLE

Toschke et al. (A-17) collected data on obesity status of children ages 5–6 years and the smoking status of the mother during the pregnancy. Table below shows 3970 subjects classified as cases or noncases of obesity and also classified according to smoking status of the mother during pregnancy (the risk factor).

We wish to compare the odds of obesity at ages 5–6 among those whose mother smoked throughout the pregnancy with the odds of obesity at age 5–6 among those whose mother did not smoke during pregnancy.

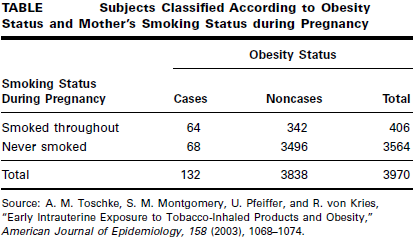
Solution

By formula:

We see that obese children (cases) are 9.62 times as likely as nonobese children (noncases) to have had a mother who smoked throughout the pregnancy.

We compute the 95 percent confidence interval for OR as follows.

The lower and upper confidence limits for the population OR, respectively, are

= 7.12 and = = 13.00

We conclude with 95 percent confidence that the population OR is somewhere between

7.12 And 13.00. Because the interval does not include 1, we conclude that, in the population, obese children (cases) are more likely than nonobese children (noncases) to have had a mother who smoked throughout the pregnancy.

PROBABILITY

Posted on June 1, 2020 by Bherulal

Measures of Dispersion

This term is used commonly to mean scatter, Deviation, Fluctuation, Spread or variability of data.

The degree to which the individual values of the variate scatter away from the average or the central value, is called a dispersion.

Types of Measures of Dispersions:

Absolute Measures of Dispersion: The measures of dispersion which are expressed in terms of original units of a data are termed as Absolute Measures.
Relative Measures of Dispersion: Relative measures of dispersion, are also known as coefficients of dispersion, are obtained as ratios or percentages. These are pure numbers independent of the units of measurement and used to compare two or more sets of data values.

Absolute Measures

Range
Quartile Deviation
Mean Deviation
Standard Deviation

Relative Measure

Co-efficient of Range
Co-efficient of Quartile Deviation
Co-efficient of mean Deviation
Co-efficient of Variation.

The Range:

1. The range is the simplest measure of dispersion. It is defined as the difference between the largest value and the smallest value in the data:

2. For grouped data, the range is defined as the difference between the upper class boundary (UCB) of the highest class and the lower class boundary (LCB) of the lowest class.

MERITS OF RANGE:-

Easiest to calculate and simplest to understand.
Gives a quick answer.

DEMERITS OF RANGE:-

It gives a rough answer.
It is not based on all observations.
It changes from one sample to the next in a population.
It can’t be calculated in open-end distributions.
It is affected by sampling fluctuations.
It gives no indication how the values within the two extremes are distributed

Quartile Deviation (QD):

1. It is also known as the Semi-Interquartile Range. The range is a poor measure of dispersion where extremely large values are present. The quartile deviation is defined half of the difference between the third and the first quartiles:

QD = Q₃ – Q₁/2

Inter-Quartile Range

The difference between third and first quartiles is called the ‘Inter-Quartile Range’.

IQR = Q₃ – Q₁

Mean Deviation (MD):

1. The MD is defined as the average of the deviations of the values from an average:

It is also known as Mean Absolute Deviation.

2. MD from median is expressed as follows:

3. for grouped data:

Mean Deviation:

The MD is simple to understand and to interpret.
It is affected by the value of every observation.
It is less affected by absolute deviations than the standard deviation.
It is not suited to further mathematical treatment. It is, therefore, not as logical as convenient measure of dispersion as the SD.

The Variance:

Mean of all squared deviations from the mean is called as variance
(Sample variance=S²; population variance= σ²sigma squared (standard deviation squared). A high variance means most scores are far away from the mean, a low variance indicates most scores cluster tightly about the mean.

Variance2JPG Formula

OR S² =

Calculating variance: Heart rate of certain patient is 80, 84, 80, 72, 76, 88, 84, 80, 78, & 78. Calculate variance for this data.

Solution:

Step 1:

Find mean of this data

= 800/10 Mean = 80

Step 2:

Draw two Columns respectively ‘X’ and deviation about mean (X-

). In column ‘X’ put all values of X and in (X-

) subtract each ‘X’ value with

.

Step 3:

Draw another Column of (X-

)², in which put square of deviation about mean.

(X-

)

Deviation about mean

(X-

)²

Square of Deviation about mean

80 – 80 = 0

84 – 80 = 4

80 – 80 = 0

72 – 80 = -8

76 – 80 = -4

88 – 80 = 8

84 – 80 = 4

80 – 80 = 0

78 – 80 = -2

0 x 0 = 00

4 x 4 = 16

0 x 0 = 00

-8 x -8 = 64

-4 x -4 = 16

8 x 8 = 64

4 x 4 = 16

0 x 0 = 00

-2 x -2 = 04

∑X = 800

= 80

∑(X-

) = 0

Summation of Deviation about mean is always zero

∑(X-

)2 = 184

Summation of Square of Deviation about mean

Step 4

Apply formula and put following values

∑(X-

)²= 184

n = 10

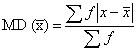
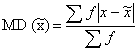
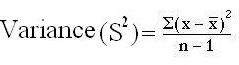Variance2JPG

Variance = 184/ 10-1 = 184/9

Variance = 20.44

Standard Deviation

The SD is defined as the positive Square root of the mean of the squared deviations of the values from their mean.
The square root of the variance.
It measures the spread of data around the mean. One standard deviation includes 68% of the values in a sample population and two standard deviations include 95% of the values & 3 standard deviations include 99.7% of the values
The SD is affected by the value of every observation.
In general, it is less affected by fluctuations of sampling than the other measures of dispersion.
It has a definite mathematical meaning and is perfectly adaptable to algebraic treatment.

Formula:

OR S =

Calculating Standard Deviation (we use same example): Heart rate of certain patient is 80, 84, 80, 72, 76, 88, 84, 80, 78, & 78. Calculate standard deviation for this data.

SOLUTION:

Step 1: Find mean of this data

= 800/10 Mean = 80

Step 2:

Draw two Columns respectively ‘X’ and deviation about mean (X-). In column ‘X’ put all values of X and in (X-) subtract each ‘X’ value with.

Step 3:

Draw another Column of (X-
)², in which put square of deviation about mean.

(X-

)

Deviation about mean

(X-

Square of Deviation about mean

80 – 80 = 0

84 – 80 = 4

80 – 80 = 0

72 – 80 = -8

76 – 80 = -4

88 – 80 = 8

84 – 80 = 4

80 – 80 = 0

78 – 80 = -2

0 x 0 = 00

4 x 4 = 16

0 x 0 = 00

-8 x -8 = 64

-4 x -4 = 16

8 x 8 = 64

4 x 4 = 16

0 x 0 = 00

-2 x -2 = 04

∑X = 800

= 80

∑(X-

) = 0

Summation of Deviation about mean is always zero

∑(X-

)2 = 184

Summation of Square of Deviation about mean

Step 4

Apply formula and put following values

∑(X-

)2 = 184

n = 10

MERITS AND DEMERITS OF STD. DEVIATION

Std. Dev. summarizes the deviation of a large distribution from mean in one figure used as a unit of variation.
It indicates whether the variation of difference of a individual from the mean is real or by chance.
Std. Dev. helps in finding the suitable size of sample for valid conclusions.
It helps in calculating the Standard error.

DEMERITS-

It gives weightage to only extreme values. The process of squaring deviations and then taking square root involves lengthy calculations.

Relative measure of dispersion:

(a) Coefficient of Variation,

(b) Coefficient of Dispersion,

(d) Mean Coefficient of Dispersion.

Coefficient of Variation (CV):

1. Coefficient of variation was introduced by Karl Pearson. The CV expresses the SD as a percentage in terms of AM:

—————- For sample data

————— For population data

It is frequently used in comparing dispersion of two or more series. It is also used as a criterion of consistent performance, the smaller the CV the more consistent is the performance.
The disadvantage of CV is that it fails to be useful when

is close to zero.
It is sometimes also referred to as ‘coefficient of standard deviation’.
It is used to determine the stability or consistency of a data.
The higher the CV, the higher is instability or variability in data, and vice versa.

Coefficient of Dispersion (CD):

If X_m and X_n are respectively the maximum and the minimum values in a set of data, then the coefficient of dispersion is defined as:

Coefficient of Quartile Deviation (CQD):

1. If Q₁ and Q₃ are given for a set of data, then (Q₁ + Q₃)/2 is a measure of central tendency or average of data. Then the measure of relative dispersion for quartile deviation is expressed as follows:

CQD may also be expressed in percentage.

Mean Coefficient of Dispersion (CMD):

The relative measure for mean deviation is ‘mean coefficient of dispersion’ or ‘coefficient of mean deviation’:

——————– for arithmetic mean

——————– for median

Percentiles and Quartiles

The mean and median are special cases of a family of parameters known as location parameters. These descriptive measures are called location parameters because they can be used to designate certain positions on the horizontal axis when the distribution of a variable is graphed.

Percentile:

Percentiles are numerical values that divide an ordered data set into 100 groups of values with at the most 1% of the data values in each group. There can be maximum 99 percentile in a data set.
A percentile is a measure that tells us what percent of the total frequency scored at or below that measure.

Percentiles corresponding to a given data value: The percentile in a set corresponding to a specific data value is obtained by using the following formula

Number of values below X + 0.5

Percentile = ——————————————–

Number of total values in data set

Example: Calculate percentile for value 12 from the following data

13 11 10 13 11 10 8 12 9 9 8 9

Solution:

Step # 01: Arrange data values in ascending order from smallest to largest

S. No	1	2	3	4	5	6	7	8	9	10	11	12
Observations or values	8	8	9	9	9	10	10	11	11	12	13	13

Step # 02: The number of values below 12 is 9 and total number in the data set is 12

Step # 03: Use percentile formula

9 + 0.5

Percentile for 12 = ——— x 100 = 79.17%

It means the value of 12 corresponds to 79^th percentile

Example2: Find out 25^th percentile for the following data

6 12 18 12 13 8 13 11

10 16 13 11 10 10 2 14

SOLUTION

Step # 01: Arrange data values in ascending order from smallest to largest

S. No	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
Observations or values	2	6	8	10	10	10	11	11	12	12	13	13	13	14	16	18

Step # 2 Calculate the position of percentile (n x k/ 100). Here n = No: of observation = 16 and k (percentile) = 25

16 x 25 16 x 1

Therefore Percentile = ———- = ——— = 4

100 4

Therefore, 25^th percentile will be the average of values located at the 4^th and 5^th position in the ordered set. Here values for 4^th and 5^th correspond to the value of 10 each.

(10 + 10)

Thus, P₂₅ (=P_k) = ————– = 10

Quartiles

These are measures of position which divide the data into four equal parts when the data is arranged in ascending or descending order. The quartiles are denoted by Q.

quartile

Quartiles	Formula for Ungrouped Data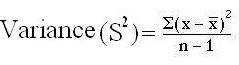	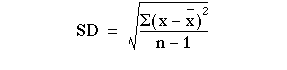Formula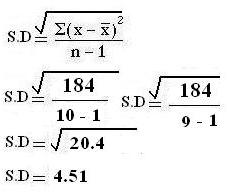 for Grouped Data
Q₁ = First Quartile below which first 25% of the observations are present
Q₂ = Second Quartile below which first 50% of the observations are present. It can easily be located as the median value.
Q₃ = Third Quartile below which first 75% of the observations are present

Symbol Key:

NORMAL DISTRIBUTION

Posted on June 1, 2020 by Bherulal

PROBABILITY

Probability:

Probability is used to measure the ‘likelihood’ or ‘chances’ of certain events (pre-specified outcomes) of an experiment.

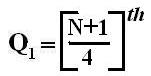
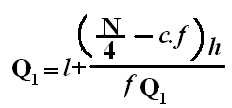
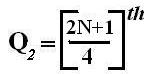
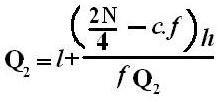
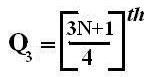
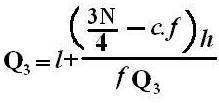
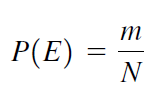If an event can occur in N mutually exclusive and equally likely ways, and if m of these possess a trait E, the probability of the occurrence of E expressed as: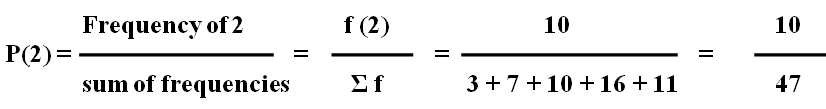

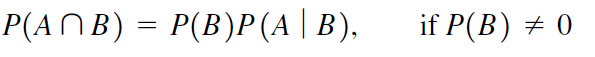Number of favourable cases

Total number of outcome (sample Space)

Characteristics of probability:

It is usually expressed by the symbol ‘P’
It ranges from 0 to 1
When P = 0, it means there is no chance of happening or impossible.
If P = 1, it means the chances of an event happening is 100%.
The total sum of probabilities of all the possible outcomes in a sample space is always equal to one (1).
If the probability of occurrence is p(o)= A, then the probability of non-occurrence is 1-A.

Terminology

Random Experiment:

Any natural phenomenon, yielding some result will be termed as random experiment when it is not possible to predict a particular result to turn out.

An Outcome:

The result of an experiment in all possible form are said to be event of that experiment. e.g. When you toss a coin once, you either get head or tail.

A trial:

This refers to an activity of carrying out an experiment like tossing a coin or rolling a die or dices.

Sample Space:

A set of All possible outcomes of a probability experiment.

Example 1: In tossing a coin, the outcomes are either Head (H) or tail (T) i.e. there are only two possible outcomes in tossing a coin. The chances of obtaining a head or a tail are equal. It can be solved as follow;

n(s) = 2 ways

S = {H, T}

Example 2: what is sample space when single dice is rolled?

n(s) = 6 ways

S = {1, 2, 3, 4, 5, 6}

A Simple Event

In an experimental probability, an event with only one outcome is called a simple event.

Compound Events

When two or more events occur in connection with each other, then their simultaneous occurrence is called a compound event.

Mutually exhaustive:

If in an experiment the occurrence of one event prevents or rules out the happening of all other events in the same experiment then these event are said to be mutually exhaustive events.

Mutually exclusive:

Two events are said to be mutually exclusive if they cannot occur simultaneously.

Example: tossing a coin, the events head and tail are mutually exclusive because if the outcome is head then the possibilities of getting a tail in the same trial is ruled out.

Equally likely events:

Events are said to be equally likely if there is no reason to expect any one in preference to other.

Example: in a single cast of a fair die each of the events 1, 2, 3, 4, 5, 6 is equally likely to occur.

Favourable case:

The cases which ensure the occurrence of an event are said to be favourable to the events.

Independent event:

When the experiments are conducted in such a way that the occurrence of an event in one trial does not have any effect on the occurrence of the other events at a subsequent experiment, then the events are said to be independent.

Example:

If we draw a card from a pack of cards and again draw a second a card from the pack by replacing the first card drawn, the second draw is known as independent f the first.

Dependent Event:

When the experiments are conducted in such a way that the occurrence of an event in one trial does have some effect on the occurrence of the other events at a subsequent experiment, then the event are said to be dependent event.

Example:

If we draw a card from a pack and again draw a card from the rest of pack of cards (containing 51 cards) then the second draw is dependent on the first.

Conditional Probability:

The probability of happening of an event A, when it is known that B has already happened, is called conditional probability of A and is denoted by P (A/B) i.e.

P(A/B) = conditional probability of A given that B has already occurred.
P (A/B) = conditional Probability of B given that A has already occurred.

Types of Probability:

The Classical or mathematical:

Probability is the ratio of the number of favorable cases as compared to the total likely cases.

The probability of non-occurrence of the same event is given by {1-p (occurrence)}.

The probability of occurrence plus non-occurrence is equal to one.

If probability occurrence; p (O) and probability of non-occurrence (O’), then p(O)+p(O’)=1.

Statistical or Empirical

Empirical probability arises when frequency distributions are used. For example:

Observation ( X)	0	1	2	3	4
Frequency ( f)	3	7	10	16	11

The probability of observation (X) occurring 2 times is given by the formulae

RULES OF PROBABILITY

Addition Rule

Rule 1: When two events A and B are mutually exclusive, then probability of any one of them is equal to the sum of the probabilities of the happening of the separate events;

Mathematically:

P (A or B) =P (A) +P (B)

Example: When a die or dice is rolled, find the probability of getting a 3 or 5.

Solution: P (3) =1/6 and P (5) =1/6.

Therefore P (3 or 5) = P (3) + P (5) = 1/6+1/6 =2/6=1/3.

2) Rule 2: If A and B are two events that are NOT mutually exclusive, then

P (A or B) = P(A) + P(B) – P(A and B), where A and B means the number of outcomes that event A and B have in common.

Given two events A and B, the probability that event A, or event B, or both occur is equal to the probability that event A occurs, plus the probability that event B occurs, minus the probability that the events occur simultaneously.

Example: When a card is drawn from a pack of 52 cards, find the probability that the card is a 10 or a heart.

Solution: P (10) = 4/52 and P (heart) =13/52

P (10 that is Heart) = 1/52

P (A or B) = P (A) +P (B)-P (A and B) = 4/52 _ 13/52 – 1/52 = 16/52.

Multiplication Rule

Rule 1: For two independent events A and B, then

P (A and B) = P (A) x P (B).

Example: Determine the probability of obtaining a 5 on a die and a tail on a coin in one throw.

Solution: P (5) =1/6 and P (T) =1/2.

P (5 and T) = P (5) x P (T) = 1/6 x ½= 1/12.

Rule 2: When two events are dependent, the probability of both events occurring is P (A and B) =P (A) x P (B|A), where P (B|A) is the probability that event B occurs given that event A has already occurred.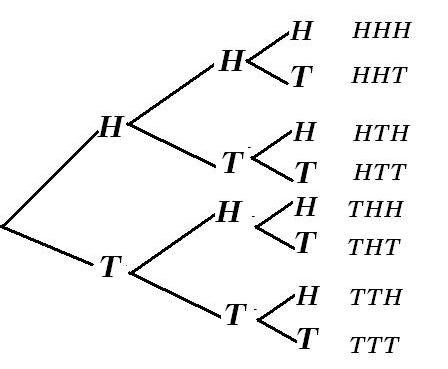

Example: Find the probability of obtaining two Aces from a pack of 52 cards without replacement.

Solution: P (Ace) =2/52 and P (second Ace if NO replacement) = 3/51

Therefore P (Ace and Ace) = P (Ace) x P (Second Ace) = 4/52 x 3/51 = 1/221

Construct sample space, when two dice are rolled

n(s) = n₁ x n₂ = 6 x 6 = 36

(1,1)	(2,1)	(3,1)	(4,1)	(5,1)	(6,1)
(1,2)	(2, 2)	(3, 2)	(4, 2)	(5, 2)	(6, 2)
(1, 3)	(2, 3)	(3, 3)	(4, 3)	(5, 3)	(6, 3)
(1, 4)	(2, 4)	(3, 4)	(4, 4)	(5, 4)	(6, 4)
(1, 5)	(2, 5)	(3, 5)	(4, 5)	(5, 5)	(6, 5)
(1, 6)	(2, 6)	(3, 6)	(4, 6)	(5, 6)	(6, 6)

EXAMPLE OF FINDING PROBABILITY OF AN EVENT

If 3 coins are tossed together, construct a tree diagram & find the followings;

a) Event showing No head b) Event showing 01 head,

c) Event showing 02 heads d) Event showing 03 heads

n (s) = n₁ x n₂ x n₃

= 2 x 2 x2 = 8

1. Event showing no head = P(X = 0)

Answer: TTT, 1/8 = 0.125

1. Event showing 01 head = P(X = 1)

Answer: HTT, THT, TTH 3/8 = 0.375

1. Event showing 02 heads = P(X = 2)

Answer: HHT, HTH, THH 3/8 = 0.375

1. Event showing 03 heads = P(X = 3)

Answer: HHH 1/8 = 0.125

Complementary Events

Complementary events happen when there are only two outcomes, like getting a job, or not getting a job. In other words, the complement of an event happening is the exact opposite: the probability of it not happening.

The probability of not occurrence of an event.

The probability of an event A is equal to 1 minus the probability of its complement, which is written as Ā and

P (Ā) = 1 – P (A)

CONDITIONAL PROBABILITY &SCREENING TESTS

Sensitivity, Specificity, and Predictive Value Positive and Negative

In the health sciences field a widely used application of probability laws and concepts is found in the evaluation of screening tests and diagnostic criteria. Of interest to clinicians is an enhanced ability to correctly predict the presence or absence of a particular disease from knowledge of test results (positive or negative) and/or the status of presenting symptoms (present or absent). Also of interest is information regarding the likelihood of positive and negative test results and the likelihood of the presence or absence of a particular symptom in patients with and without a particular disease.

In consideration of screening tests, one must be aware of the fact that they are not always infallible. That is, a testing procedure may yield a false positive or a false negative.

False Positive:

A false positive results when a test indicates a positive status when the true status is negative.

False Negative:

A false negative results when a test indicates a negative status when the true status is positive.

Sensitivity:

The sensitivity of a test (or symptom) is the probability of a positive test result (or presence of the symptom) given the presence of the disease.

Specificity:

The specificity of a test (or symptom) is the probability of a negative test result (or absence of the symptom) given the absence of the disease.

Predictive value positive:

The predictive value positive of a screening test (or symptom) is the probability that a subject has the disease given that the subject has a positive screening test result (or has the symptom).

Predictive value negative:

The predictive value negative of a screening test (or symptom) is the probability that a subject does not have the disease, given that the subject has a negative screening test result (or does not have the symptom).

Summary of formulae:

Symbols

COUNTING RULES

1) FACTORIALS (number of ways)

The result of multiplying a sequence of descending natural numbers down to a number. It is denoted by “!”

Examples:

4! = 4 × 3 × 2 × 1×0! = 24

7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040

Remember : 0! = 1

General Method:

n! = n (n -1) (n -2) (n -3)……….. (n – n)!

2) PERMUTATION RULES

All possible arrangements of a collection of things, where the order is important in a subset.

Repetition of same items with different arrangement is allowed.

Examples

COMBINATIONS

The order of the objects in a subset is immaterial.

Repetition of same objects in not allowed with different arrangement

Examples:

Binomial distribution:

Binomial distribution is a probability distribution which is obtained when the probability ‘P’ of the happening of an event is same in all the trials and there are only two event in each trial.

Conditions:

Each trial results in one of two possible, mutually exclusive, outcomes. One of the possible outcomes is denoted (arbitrarily) as a success, and the other is denoted a failure.
The probability of a success, denoted by p, remains constant from trial to trial. The probability of a failure (1 – p) is denoted by q.
The trials are independent; that is, the outcome of any particular trial is not affected by the outcome of any other trial.
Parameter should be available; (n & p) are parameters.

Formula:

b (X: n, p) = ⁿC_x p^x q^{n – x} (OR) f (x) = ⁿC_x p^x q^{n – x}

Where

X = Random variable

n = Number of Trials

p = Probability of Success

q = Probability of Failure

Measure of Central Tendency

Posted on June 1, 2020 by Bherulal

Measure of Central Tendency

Central tendency or central position or statistical averages reflects the central point or the most characteristic value of a set of measurements. The measure of central tendency describes the one score that best represents the entire distribution,

(OR)

A single figure that describes the entire series of observations with their varying sizes, occupying a central position.

The most common measures of central tendency are

Mean
Median
Mode

Characteristics of Central Tendency:

It should be rigidly defined
An average should be properly defined so that it has one and only one interpretation.
The average should not depend on the personal prejudice and bias of the investigator.
It should be based onall items
It should be easily understand.
It should not be unduly affected by the extreme value.
It should be least affected by the fluctuation of the sampling.
It should be easy to interpret.
It should be easily subjected to further mathematical calculations.

Measure of Central Tendency

If n ≤ 15

Direct Method

If n > 15

Frequency Distribution Method

Simple /Ungrouped Frequency Distribution

(Range ≤ 20 digits)

Grouped Frequency Distribution

(Range > 20 digits)

Mean:

It is defined as a value which is obtained by dividing the sum of all the values by the numbers of observations. Thus arithmetic mean of a set of values x₁, x₂, x₃, x_4.. . . .x_n is denoted by (read as “x bar”) and is calculated as:

= = (Direct Method)

Where sign ∑ stands for the sum and “n” is the number of observations.

Example:

The grades of a student in five examinations were 67, 75, 81, 87, 90 find the arithmetic mean of grades.

Solution:

Here, = = 80

Thus, the mean grade is 80.

Method of Finding Mean

If x₁, x₂, x₃, x₄, ….x_n are the values of different observations andf₁, f₂, f₃, f₄, ….f_nare their frequencies_,then,

Or. A.M. =

Example 2. The number of children of 80 families in a village are given below:

No. of Children/Family	1	2	3	4	5	6
No. of Families	8	10	10	25	20	7

Calculate mean.

Solution: let x_i represent the number of children per family and f_i represent the number of families. The calculations are presented in the following table:

No. of Children/Family (x_i)	No. of Families (f_i)	f_ix_i
1	8	8
2	10	20
3	10	30
4	25	100
5	20	100
6	7	42
	n=∑f_i =80	∑f_ix_i = 300

Thus = = = 3.75

Methods of Finding Arithmetic mean for Grouped Data

Let x₁, x₂, x₃, x_4.. . . .x_nbe mid-points of the class intervals with corresponding frequencies f₁, f₂, f₃, f₄, ….f_n . Then the arithmetic mean is obtained by dividing the sum of the product of “f “ and “x” by the total of all frequencies.

Thus:

A.M. = =

Example:

Given below are the heights of (in inches) of 200 students. Find A.M.

Height (inches)	30-35	35-40	40-45	45-50	50-55	55-60
No. of Students	28	32	36	46	36	22

Solution:

Height (Inches)	Mid points (x)	Frequency (f)	fx
30-35	32.5	28	910
35-40	37.5	32	1200
40-45	42.5	36	1530
45-50	47.5	46	2185
50-55	52.5	36	1890
55-60	57.5	22	1265
Total:	—	∑f = 200	∑fx = 8980

= = = 44.90 (inches).

Example: Given below are the weights (in kgs) of 100 students. Find Mean Weight:

Weight	70-74	75-79	80-84	85-89	90-94
No. of Students	10	24	46	12	8

Solution:

Weight (Kg)	Mid-Points (x)	Frequency (f)	fx
70 – 74	72	10	720
75 – 79	77	24	1848
80 – 84	82	46	3772
85 – 89	87	12	1044
90 – 94	92	8	736
Total:	—	∑f = 100	∑fx = 8120

= = = 81.20

Here, Mean Weight is 31.2 kgs.

Merits of Mean

It has the simplest average formula which is easily understandable and easy to compute.
It is so rigidly defined by mathematical formula that everyone gets same result for single problem.
Its calculation is based on all the observations.
It is least affected by sampling fluctuations.
It is a typical i.e. it balances the value at either side.
It is the best measure to compare two or more series.(data)
Mean is calculated on value and does not depend upon any position.
Mathematical centre of a distribution
Good for interval & ratio scale
Does not ignore any information
Inferential statistics is based on mathematical properties of the mean.
It is based on all the observations.
It is easy to calculate and simple to understand.
It is relatively stable and amendable to mathematical treatment.

Demerits of Mean

It cannot be calculated if all the values are not known.
The extreme values have greater affect on it.
It cannot be determined for the qualitative data.
It may not exist in data.

Median:

It is the middle most point or the central value of the variable in a set of observation when observations are arranged in either order of their magnitudes.

It is the value in a series, which divides the series into two equal parts, one consisting of all values less and the other all values greater than it.

Median for Ungrouped data

Median of “n” observations, x₁, x₂, x₃,…x_n can be obtained as follows:

When “n” is an odd number,

Median = ()^th observation

When “n” is an even number,

Median is the average of ()^thand ()^thobservations.

Simply use ()th observation. It will the average

The median for the discrete frequency distribution can be obtained as above, Using a cumulative frequency distribution.

Problem

Find the median of the following data:

12, 2, 16, 8, 14, 10, 6

Step 1: Organize the data, or arrange the numbers from smallest to largest.

2, 6, 8, 10, 12, 14, 16

Step 2: count number of observation in data (n)

.n = 7

Step 3: Since the number of data values is odd, the median will be found in the position.

Median term (m) =

7 + 1 8

= = = 4^th value

2 2

Step 4: In this case, the median is the value that is found in the fourth position of the organized data, therefore

Median = 10

Problem

Median for even data:

Find the median of the following data:

7, 9, 3, 4, 11, 1, 8, 6, 1, 4

Step 1: Organize the data, or arrange the numbers from smallest to largest.

1, 1, 3, 4, 4, 6, 7, 8, 9, 11

Step 2: Since the number of data values is even, the median will be the mean value of the numbers found before and after the

position.

Step 3: The number found before the 5.5 position is 4 and the number found after the 5.5 position is 6. Now, you need to find the mean value.

1, 1, 3, 4, 4, 6, 7, 8, 9, 11

Example:

The following are the runs made by a batsman in 7 matches:

8, 12, 18, 13, 16, 5, 20.Find the median.

Solution: Writing the runs in ascending order.

5, 8, 12, 13, 16, 18, 20

As n=7

Median= ()^thitem = ()4^th item.

Hence, Median is13 runs.

Example:

Following are the marks (out of 100) obtained by 10 students in English:

23, 15, 35, 41, 48, 5, 8, 9, 11, 51. Find the median mark.

Solution: arranging the marks in ascending order. The marks are:

5, 8, 9, 11, 15, 23, 35, 41, 48, 51

As n= 10

So, median = [] item.

Or, Median = [15+23] = = 19 marks.

Alternative Method:

Median term(m) = ()^th value

= 11/2 = 5.5^th value

5, 8, 9, 11, 15, 23, 35, 41, 48, 51

M1 M2

Median =

Median = = 19

Median for Grouped data

It is obtained by the following formula:

Median = l₁ +()

Where, l₁ = lower class limit of median class.

l₂ = upper class limit of median class

f = frequency of median class.

m = or

C = cumulative frequency preceding the median class.

n = total frequency, i.e. ∑f.

Example:

Find the median height of 200 students in given data

Solution:

Class interval	Frequency (f)	C.F
30-35	28	28
35-40	32	28+32=60
40-45	36	60+36=96
45-50	46	96+46=142
50-55	36	142+36=178
55-60	22	178+22=200 n

Median =

As 100.5 ^th item lies in (45-50), it is the median class with l₁ = 45, l₂= 50 ,f= 46, C= 96

Median = l₁ +()

Median = 45 + (

= 45 +

= 45 + 0.489

= 45.489

Thus, median height is 45.489 inches.

2^nd Method:

l + (

Where, l = lower class boundary of median class.

w = width of median class.

f = frequency of median class.

n = total frequency, i.e. ∑f.

c = cumulative frequency preceding the median class.

Example:

Following are the weights in kgs of 100 students. Find the median weight.

Weights (kgs)	70-74	75-79	80-84	85-89	90-94
No of students.	10	24	46	12	8

Solution: As class boundaries are not given so, first of all we make class boundaries by using procedure.

Weight (kgs)	No. of students	Class boundaries	C.F
70-74	10	69.5-74.5	10
75-80	24	74.5-79.5	34
80-84	46	79.5-84.5	80
85-89	12	84.5-89.5	92
90-94	8	89.5-94.5	100

Median =

As 50^th item lies in (79.5-84.5), it is the median class with h= 5, f= 46, C= 34

Median = l + (, we find

Median = 79.5 + (

= 79.5 +

Hence, median weight is 81.24 kg.

Merits of Median:

It is easily understood although it is not so popular as mean.
It is not influenced or affected by the variation in the magnitude or the extremes items.
The value of the median can be graphically ascertained by ogives.
It is the best measure for qualitative data such as beauty, intelligence etc.
The median indicated the value of middle item in the distribution i.e. middle most item is the median
It can be determined even by inspection in many cases.
Good with ordinal data
Easier to compute than the mean

Demerits of Median:

For the calculation of median, data must be arranged.
Median being a positional average, cannot be dependent on each and every observations.
It is not subject to algebraic treatment.
Median is more affected or influenced by samplings fluctuations that the arithmetic mean.
May not exist in data.
It is not rigorously defined.
It does not use values of all observations.

Mode:

Mode is considered as the value in a series which occurs most frequently (has the highest frequency)

The mode of distribution is the value at the point around which the items tend to be most heavily concentrated. It may be regarded as the most typical value.

The word modal is often used when referring to the mode of a data set.
If a data set has only one value that occurs most often, the set is called unimodal.
A data set that has two values that occur with the same greatest frequency is referred to as bimodal.
When a set of data has more than two values that occur with the same greatest frequency, the set is called multimodal.

Mode for Ungrouped data

Example 1. The grades of Jamal in eight monthly tests were 75, 76, 80, 80, 82, 82, 82, 85.Find the mode of his grades.

Solution: As 82 is repeated more than any other number, so clearly mode is 82.

Example 2. Ten students were asked about the number of questions they have solved out of 20 questions, last week. Records were 13, 14, 15, 11, 16, 10, 19, 20, 18, 17. Find the modes.

Solution: it is obvious that the data contain no mode, as none of the numbers is repeated. Sometimes data contains several modes.

If x = 10, 15, 15, 15, 20, 20, 20, 25 then the data contains two modes i.e. 15 and 20.

Mode for grouped data

Mode for the grouped data can be calculated by the following formula:

Mode=

(OR)

Mode=

(OR)

Mode=

l₁= lower limit (class boundary) of the modal class.

l₂ = upper limit of the modal class

f_m= frequency of the modal class

f₁= frequency associated with the class preceding the modal class.

f₂ = frequency associated with the class following the modal class

h = (size of modal class)

The class with highest frequency is called the “Modal Class”.

Example 3. Find the mode for the heights of 200 students in given data

Height (inches)	Frequency
30-35	28
35-40	32
40-45	36 ()
45-50	46 ()
50-55	36 ()
55-60	22
	∑f=200

Solution:

Mode=

Mode = 47. 5

Merits of Mode:

It can be obtained by inspection.
It is not affected by extreme values.
This average can be calculated from open end classes.
The score comes from the data set
Good for nominal data
Good when there are two ‘typical‘ scores
Easiest to compute and understand
It can be used to describe qualitative phenomenon
The value of mode can also be found graphically.

Demerits of Mode

Mode has no significance unless a large number of observations are available.
It cannot be treated algebraically.
It is a peculiar measure of central tendency.
For the calculation of mode, the data must be arranged in the form of frequency distribution.
It is not rigidly define measure.
Ignores most of the information in a distribution
Small samples may not have a mode.
It is not based on all the observations.

Empirical Relationship b/w

Skewness:

Data distributions may be classified on the basis of whether they are symmetric or asymmetric. If a distribution is symmetric, the left half of its graph (histogram or frequency polygon) will be a mirror image of its right half. When the left half and right half of the graph of a distribution are not mirror images of each other, the distribution is asymmetric.

If the graph (histogram or frequency polygon) of a distribution is asymmetric, the distribution is said to be skewed. The mean, median and mode do not fall in the middle of the distribution.

Types of Skewness

Positive skewness: If a distribution is not symmetric because its graph extends further to the right than to the left, that is, if it has a long tail to the right, we say that the distribution is skewed to the right or is positively skewed. In positively skewed distribution Mean > Median > Mode. The positive skewness indicates that the mean is more influenced than the median and mode, by the few extremely high value. Positively skewed distribution have positive value because mean is greater than mode
Negative skewness: If a distribution is not symmetric because its graph extends further to the left than to the right, that is, if it has a long tail to the left, we say that the distribution is skewed to the left or is negatively skewed. In negatively skewed distribution Mean < Median < Mode. Negatively skewed distribution have negative value because mean is less than mode.

KURTOSIS

Kurtosis is a measure of the degree to which a distribution is “peaked” or flat in comparison to a normal distribution whose graph is characterized by a bell-shaped appearance.

Platykurtic curve: when the frequency distribution curve is flatter than the normal bell shaped curve
Leptokurtic curve: when the frequency distribution curve is more peaked than the normal bell shaped curve
Mesokurtic curve: the normal bell shaped distribution curve.

Nursing Tutorials

Tag Archives: Biostatistics

INFERENTIAL STATISTICS

PROBABILITY

NORMAL DISTRIBUTION

Measure of Central Tendency

Method of Finding Mean

Methods of Finding Arithmetic mean for Grouped Data

Median for Ungrouped data

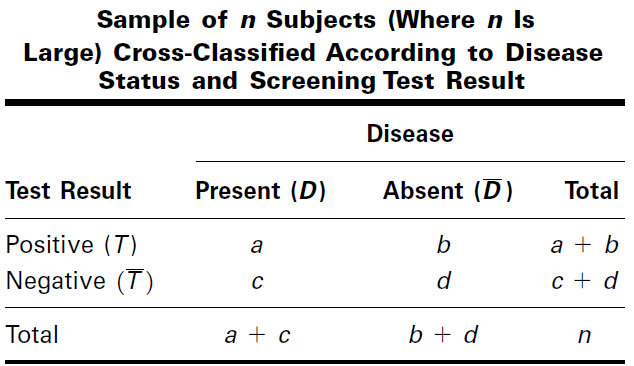
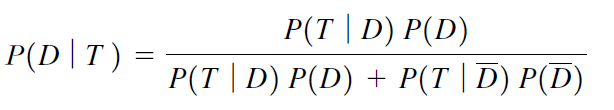
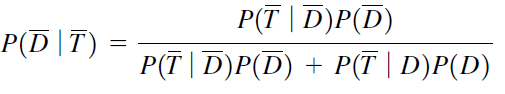
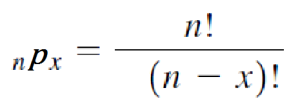
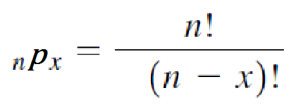Mode for Ungrouped data